- Titulní strana
- Úvod
- Pojmy a značení
- Soubory ke stažení
- 1. Úvod ke stereometrii
- 2. Základní věty
- 3. Určení přímky
- 4. Určení roviny
- 5.Vzájemné polohy
6.Polohové konstrukční úlohy
Úvod ke stereometrii, základní pojmy
Mezi základní geometrické útvary patří bod, přímka a rovina.
Stereometrie se zabývá studiem prostorových útvarů. Mezi tyto útvary patří například hranol, krychle, kužel, jehlan a další. Slovo stereometrie je řeckého původu a jeho volný překlad je měření těles.
V planimetrii leží všechny útvary v jedné rovině. Těchto rovin může být ve stereometrii nekonečně mnoho.
Mnohostěny
Název tělesa Charakteristika Obrázek Obecný n-boký hranol podstavy jsou dva shodné n-úhelníky, boční stěny jsou rovnoběžníky
speciální případ: kolmý n-boký hranol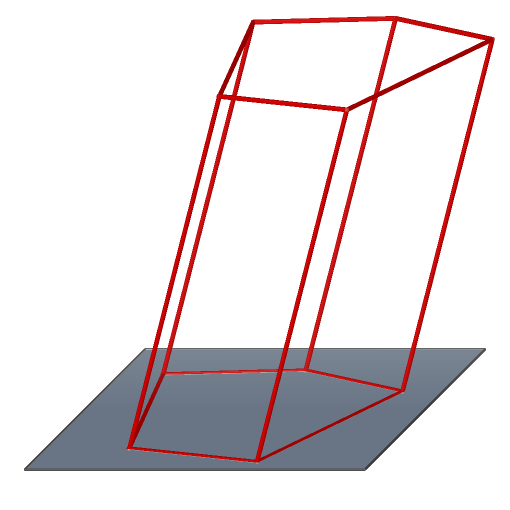
Kolmý n-boký hranol podstavy jsou n-úhelníky, boční stěny jsou obdelníky (případně čtverce) a jsou kolmé k podstavě
speciální případ: krychle, kvádr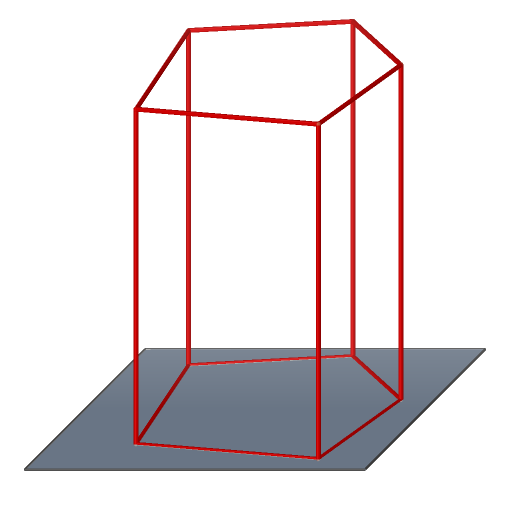
Kvádr kolmý čtyřboký hranol, každé dvě protilehlé stěny jsou shodné obdelníky 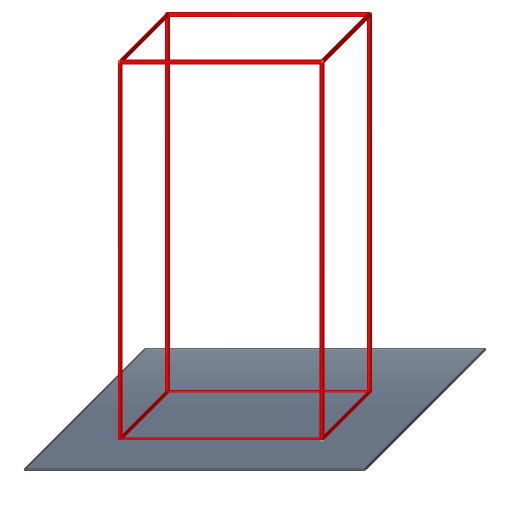
Krychle kolmý čtyřboký hranol, všechny stěny jsou shodné čtverce 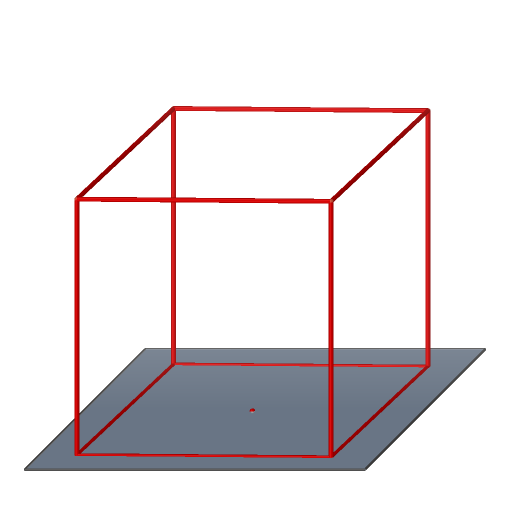
Obecný n-boký jehlan podstavou je n-úhelník, stěny jsou trojúhelníky 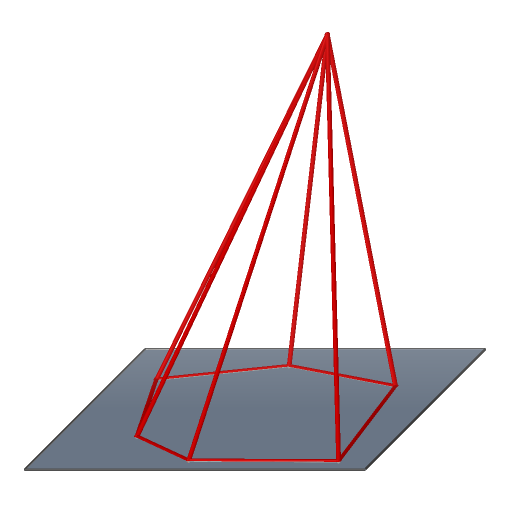
Obecný 4-boký jehlan podstavou je 4-úhelník, stěny jsou trojúhelníky
speciální případ: pravidelný čtyřboký jehlan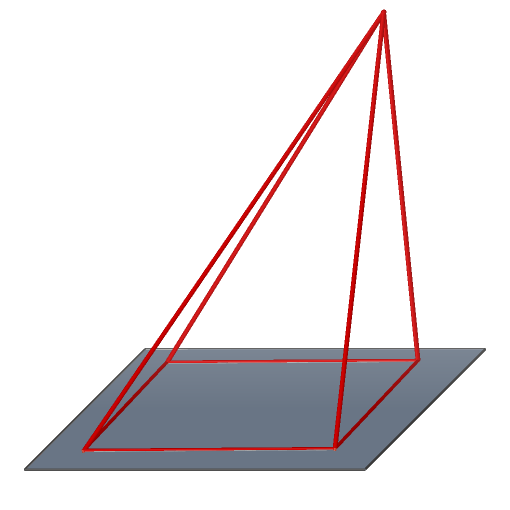
Pravidelný čtyřboký jehlan podstava je čtverec, stěny jsou shodné rovnoramenné trojúhelníky 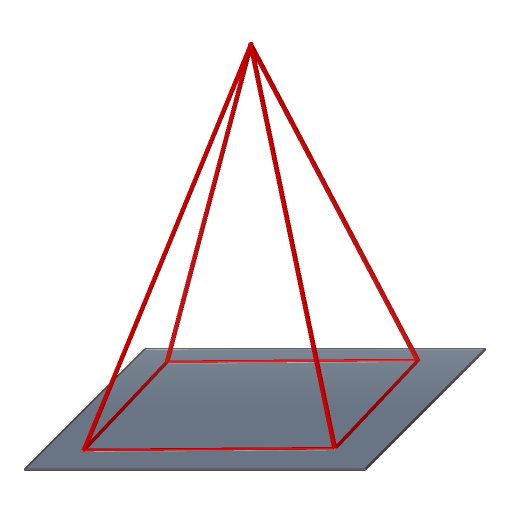
Čtyřstěn všechny čtyři stěny jsou trojúhelníky
speciální případ: pravidelný čtyřstěn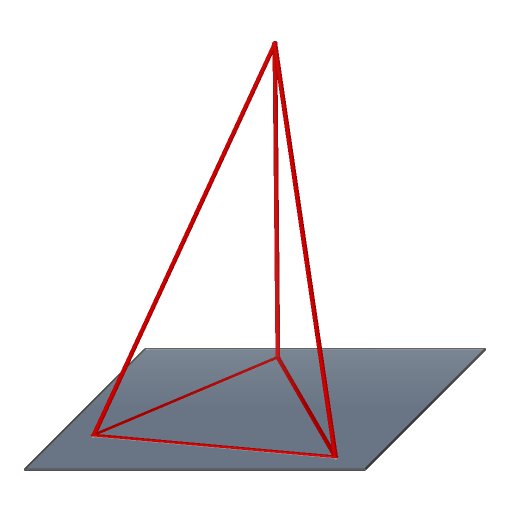
Pravidelný čtyřstěn všechny čtyři stěny jsou shodné rovnostranné trojúhelníky 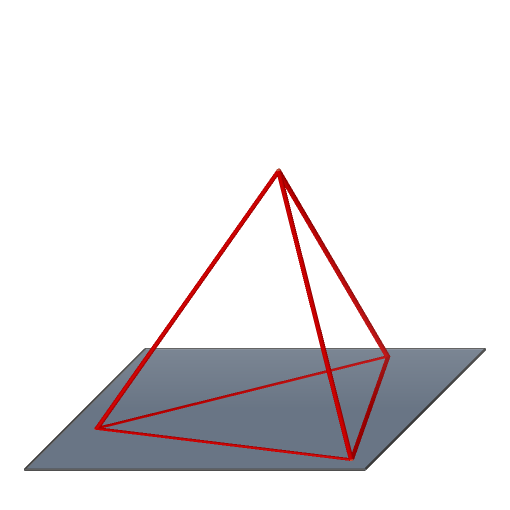
Deskriptivní geometrie
Deskriptivní geometrie je věda o zobrazení prostorových útvarů do roviny (průmětny). Podstatou deskriptivní geometrie je jednoznačný vztah mezi zobrazovaným objektem a jeho průmětem. Zjednodušeně řečeno jde o zobrazování trojrozměrných útvarů na dvojrozměrnou nákresnu. Praktické využití našla deskriptivní geometrie všude tam, kde je třeba technicky přesně zakreslit různé prostorové útvary.
Volné rovnoběžné promítání
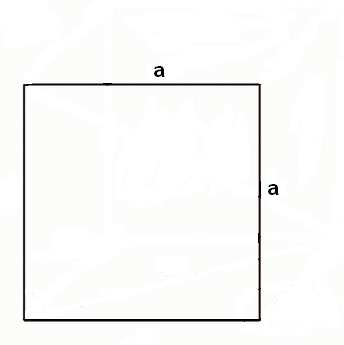
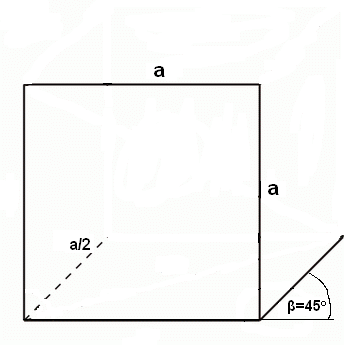
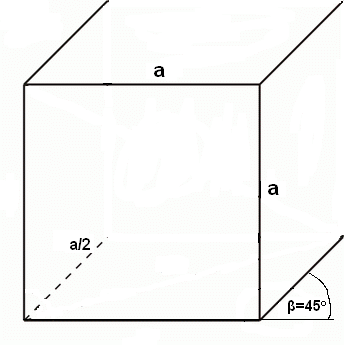
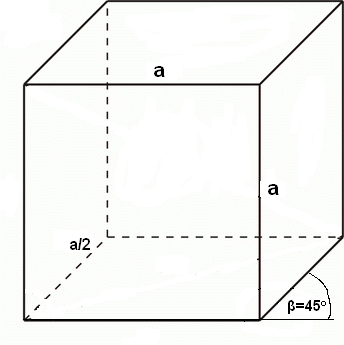
Než se pustíme do složitějších úloh jako vzájemná poloha rovin či řezy krychlí, měli bychom se naučit rovnoběžně promítnout tělesa do roviny. Na tomto promítání není v zásadě nic těžkého. Nejdříve si musíme určit průmětnu. Směr promítání je různoběžný s průmětnou. Útvary v této rovině (nebo rovnoběžné s touto rovinou) se zobrazují ve skutečné velikosti. Přímky kolmé na průmětnu se obvykle zobrazují s odchylkou 45° od vodorovného směru.
Postup promítnutí krychle ve volném rovnoběžném promítání (nadhled zprava):